
The reflecting line is the perpendicular bisector of all segments that connect pre-image locations to their corresponding image points when a figure is reflected." "text": "Ans: A perpendicular bisector is a reflecting line. The point (x,y) reflected across the x-axis is "Question", When graphing, if you forget the rules for reflections, fold the paper along the x-axis (the line of reflection) to see where the new figure will be.

How do you write a reflection over the x-axis?", "text": "Ans: The y-coordinate remains the same when a point is reflected across the y-axis, while the x-coordinate is changed into the opposite (its sign is "Question", How do you write a reflection over the y-axis?", The size and shape of the figure do not change when it is "Question", On the other side of every point in the diagram, another point is discovered precisely opposite it. "text": "Ans: When a figure is built around a single point known as the point of reflection or its centre, it becomes a reflection point. What is the reflection of a point on a graph?",

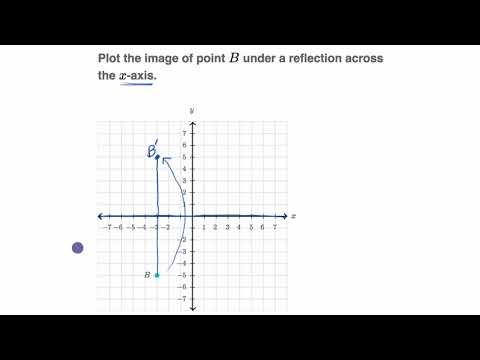
The y-coordinate remains the same when a point is reflected across the y-axis, while the x-coordinate is changed into the opposite (its sign is "Question", "text": "Ans: The x-coordinate remains the same when a point is reflected across the x-axis, while the y-coordinate is turned into the opposite (its sign is changed). How do you find the reflection of a point on a graph?", The reflecting line is the perpendicular bisector of all segments that connect pre-image locations to their corresponding image points when a figure is reflected. The point \(\left( \right).\)Īns: A perpendicular bisector is a reflecting line. \(MR \bot AA’.\) The mirror line is perpendicular bisector to the line joining the point and its image. \(OA=OA’.\) The distance of a point from the mirror is the same as the distance of its image.Ģ. If you look at the image of a point \(A\) in the mirror \(MR,\) as shown in the figure, you will find it at \(A’.\) Let \(AA’\) intersect \(MR\) at \(O.\) We find thatġ. Reflection symmetry is a concept utilised in the design of astronomical telescopes. Note: Any object’s reflected image is identical to the object itself.
The line of reflection refers to a single line that aids in the reflection of an object. Both figures (before and after reflection) are equidistant from all places on their respective surfaces.ĥ. Because the position has altered because of the transformation, there are possibilities for translation as well.Ĥ. The size and shape, however, remain the same.ģ. The only difference is that the generated image is in the opposite direction. As a result, the final image will reflect the original structure.Ģ. In geometry, flipping an image is known as a reflection.


 0 kommentar(er)
0 kommentar(er)
